Converting projections on Shapely

Sometimes when dealing with coordinates, you may need to work in meters instead of degrees, but, since we don’t live in a flat earth, the calculation is not trivial. Thankfully, there are tools to help with the conversions.

Understanting projections

Maps are a lie! We live in a spheric-ish, bumpy and irregular planet, but we need to convey geographical information on flat surfaces, and those things are not totally compatible; a map in a piece of paper of screen always is going to have some level of distortion.

There are many map projections to pick, each one with their own advantages and disadvantages: some preserve area, some preserve shapes, some are officially adopted by some countries, etc.

Oblique Mercator

For the use case of performing operations in meters and converting back into degrees, the best projection is the Oblique Mercator, this guarantees a very low distortion near its anchor point. You probably already heard about the Mercator projection, very popular on printed maps; so, Oblique Mercator is a variant where the anchor point is arbitrary, while the "normal" Mercador has its anchor pinned at “Null Island” (latitude 0, longitude 0).

Python libraries

Shapely

Shapely is a very versatile geometry library, it contains geometric objects (Point, LineString, Polygon, etc) and a huge list of methods and operations to handle them.

But notice that Shapely is a geometry library, not a geography one! That means it is just a mathematical library, operating on a cartesian plane without attaching any units. Please refer to its very comprehensive manual if you want to get deeper.

Instalation:

$ pip install shapely

pyproj

To use Shapely in a geography level, you need to combine it with pyproj: this is an interface for the PROJ library, the industry standard for all map projection transformations.

Instalation:

Before install pyproj via pip, make sure you have PROJ installed, here are the instructions.

$ pip install pyproj

Conversion functions

The conversion is not necessarily “hard”, but because PROJ is very flexible in its configuration, it can be intimidating trying to understand its documentation without some background. To make things easier, please use this snippet below, the function get_projections() returns a tuple of two functions: the first converts geodesic shapes into the shapes in the cartesian plane, and the the second do the opposite.

from functools import partial
from pyproj import Proj, Transformer
from shapely.geometry import Point
from shapely.ops import transform

def get_projections(anchor_point=None):
    if not anchor_point:  # If no anchor, set 0/0 (normal Mercator).
        anchor_point = Point(0, 0)
    crs = {
        'proj': 'omerc',
        'lat_0': anchor_point.y,
        'lonc': anchor_point.x,
        'alpha': 1e-6,
        'k': 1,
        'gamma': 0.0,
        'units': 'm',
        'ellps': 'WGS84',
        'no_defs': True,
    }
    proj = Proj(crs, preserve_units=True)
    proj_inverse = Transformer.from_proj(proj, 'EPSG:4326', always_xy=True).transform
    return partial(transform, proj), partial(transform, proj_inverse)

And this is how you use it: the anchor_point is the geodesic point that will become our 0/0 point in the cartesian plane:

>>> center_of_berlin = Point(13.409408, 52.520842)
>>> brandenburg_gate = Point(13.377701, 52.516262)
>>> geodesic_to_cartesian, cartesian_to_geodesic = get_projections(center_of_berlin)

>>> geodesic_to_cartesian(brandenburg_gate)
<POINT (-2152.435 -509.177)>  # In meters, from the center of Berlin.

>>> cartesian_to_geodesic(geodesic_to_cartesian(brandenburg_gate))
<POINT (13.378 52.516)>  # Back to degrees.

Examples

Distance between points

Steps:

• Pick the source point as the anchor for get_projections();
• Transform both points into the cartesian plane with geodesic_to_cartesian();
• Run the source.distance(destination).

Check the documentation on Shapely's distance() method.

>>> center_of_berlin = Point(13.409408, 52.520842)
>>> brandenburg_gate = Point(13.377701, 52.516262)
>>> geodesic_to_cartesian, _ = get_projections(center_of_berlin)

>>> cartesian_center_of_berlin = geodesic_to_cartesian(center_of_berlin)
>>> cartesian_brandenburg_gate = geodesic_to_cartesian(brandenburg_gate)

>>> cartesian_center_of_berlin.distance(cartesian_brandenburg_gate)
2211.8404871748057  # In meters.

Area of a polygon

Steps:

• Load a Shapely polygon;
• Pick the polygon’s centroid as the anchor for get_projections();
• Transform it into the cartesian plane with geodesic_to_cartesian();
• Run polygon.area.

Check the documentation on Shapely's area property.

You can use both the constructor for the Polygon object or load it from GeoJSON with the shape() function:

from shapely.geometry import shape

museum_island = shape({
    "type": "Polygon",
    "coordinates": [
        [
            [13.393639, 52.522081],
            [13.397824, 52.519285],
            [13.403055, 52.512100],
            [13.405072, 52.511486],
            [13.411649, 52.513873],
            [13.406418, 52.514692],
            [13.401411, 52.519580],
            [13.398160, 52.521513],
            [13.393639, 52.522081]
        ]
    ]
})

Here is the shape above rendered in a map:

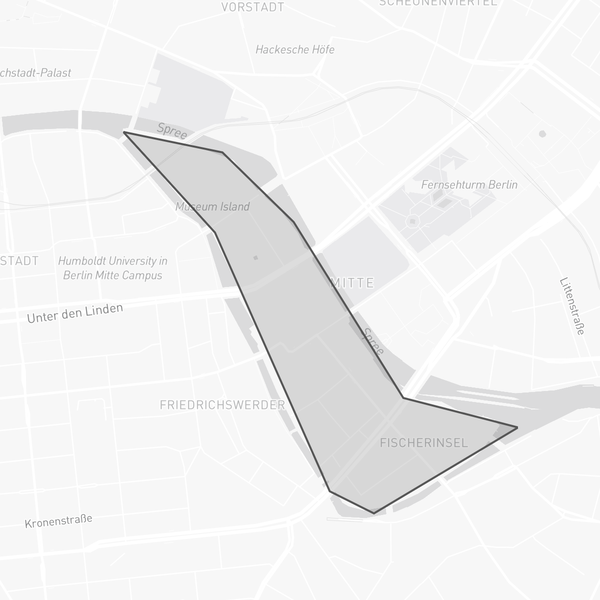
Please notice that if you get the area from a geodesic object, the value will be in degrees, that makes no sense, since the atual area varies a lot if the shape is near the equator or near the poles.

>>> geodesic_to_cartesian, _ = get_projections(museum_island.centroid)

>>> museum_island.area
5.0027242999976146e-05  # ❌ In degrees, this is NOT useful!

>>> geodesic_to_cartesian(museum_island).area
377902.9629890913  # In square meters.

>>> geodesic_to_cartesian(museum_island).area / 1_000_000
0.3779029629890913  # In square kilometers.

Radius polygon around a point

Steps:

• Pick the source point as the anchor or get_projections();
• Transform it into the cartesian plane with geodesic_to_cartesian();
• Apply a buffer() over it with your radius in meters (this returns a circular polygon);
• Convert it back with cartesian_to_geodesic();
• (Optional): Use mapping() to convert it into GeoJSON.

Check the documentation on Shapely's buffer() method.

center_of_berlin = Point(13.409408, 52.520842)
geodesic_to_cartesian, cartesian_to_geodesic = get_projections(center_of_berlin)

cartesian_center_of_berlin = geodesic_to_cartesian(center_of_berlin)
cartesian_circle = cartesian_center_of_berlin.buffer(30_000, resolution=9)  # 30Km, 36 vertices (4 * 9).
geodesic_circle = cartesian_to_geodesic(cartesian_circle)

This is how you convert the geodesic_circle object into GeoJSON with the mapping() function:

import json
from shapely.geometry import mapping

circle_geojson = json.dumps(mapping(geodesic_circle))

The content of circle_geojson looks like:

{
  "type": "Polygon",
  "coordinates": [
    [
      [13.851369517452731, 52.52001684395894], [13.84419333237743, 52.47322786545606],
      [13.82384962144716, 52.427907468142855], [13.790992602415423, 52.385426101649315],
      [13.746647020478344, 52.34706464968061], [13.692173951866176, 52.31397671258963],
      [13.629227922924512, 52.287154992445906], [13.559706799470275, 52.267402631446686],
      [13.485695926818149, 52.255310200330925], [13.40940799233307, 52.251238877281935],
      [13.333120058076762, 52.255310201955346], [13.25910918610451, 52.267402634647084],
      [13.189588063761999, 52.28715499712664], [13.126642036332331, 52.31397671861066],
      [13.072168969589173, 52.34706465686153], [13.027823389824242, 52.38542610977443],
      [12.994966373204546, 52.427907476967505], [12.974622664855207, 52.47322787471379],
      [12.967446482452836, 52.52001685336939], [12.97369737930227, 52.5668552183338],
      [12.993227388561863, 52.612317819578806], [13.025480427930086, 52.655017058880745],
      [13.069504604188237, 52.69364577761025], [13.123977621128224, 52.727018141547795],
      [13.187244976593817, 52.7541071425489], [13.25737006180486, 52.77407739795136],
      [13.332194687865442, 52.786312051983195], [13.409408007761378, 52.790432768978405],
      [13.48662132741714, 52.7863120503392], [13.561445952765052, 52.774077394714226],
      [13.63157103681411, 52.754107137818636], [13.694838390706073, 52.72701813547045],
      [13.749311405711442, 52.693645770373024], [13.79333557973581, 52.65501705070612],
      [13.825588616641758, 52.61231781071741], [13.84511862328763, 52.5668552090565],
      [13.851369517452731, 52.52001684395894]
    ]
  ]
}

And this is the same polygon rendered in a map:

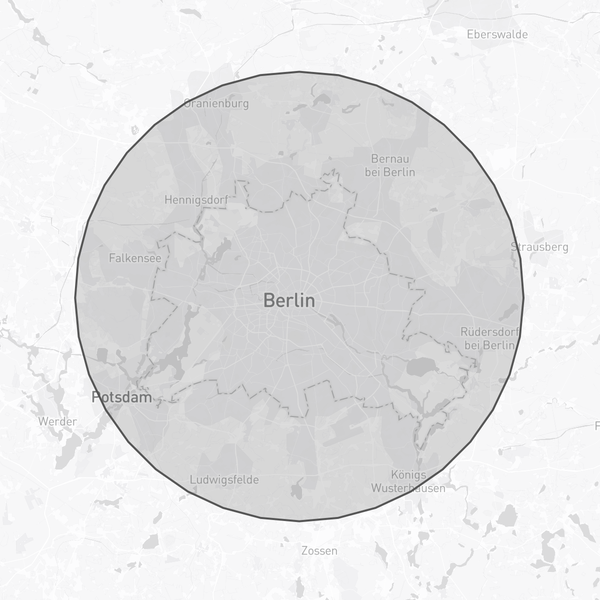
Conclusion

I hope you can find this snippet useful; feel free to use it on your projects.

The examples in this article are not even scratching the surface on Shapely, I recommend a back-to-back read on its documentation. You probably don’t need to dive as deep on PROJ, unless your project has a custom required standard to follow.

For things more advanced, the same patterns stands: convert to cartesian ➤ perform operations ➤ convert to geodesic.